Find Recurring Decimals using Vedic Math

Use Indian Vedic Techniques to excel in Math
Introduction
Hello everyone!, Welcome back to yet another post on Ekadhikina Purvena (“By one more than the previous one”).
Now that we are done with the various techniques that we used to mentally multiply large numbers using vedic math, in this post let's dive into division. This will be specifically for any rational number (or its equivalent rational number) that can be represented in the format `a/(b9)`.
Let’s understand and appreciate how vedic math principles help solve above seemingly hard recurring decimal divisions (also called as vulgar fraction). Infact, by the end of this post, you will be able to do this division mentally with higher speed.
Also what if, I say, we can also find these recurring decimal answer by performing multiplication instead of divison.
Surprised! Puzzled! just continue reading on to find the answer.
Can you do this division mentally in few seconds?
Find the value of `3/13`?
Try it the conventional way, if you want to know how time consuming it is!
How to apply Ekadhikina Purvena principle?
The below are the sequence of steps that we will perform. Later we will look into an algebraic proof for convincing us that it follows all the rules of the math realm.
Let's take an example `1/(19)` to under this method.
Initial Steps:
1. First find out if the given rational number is of the form `a/(b9)`. The given number `1/(19)` is of this format. Also note "a" should be less than "b9". Meaning, it needs to be a proper fraction.
Other Examples: `4/(29)`, `13/(109)` etc...
2. If the number is not in that format, can you convert it to an equivalent rational number that can be of that form? If so, then this method can still be applied to it. Whatever answer we get for the equivalent rational number is the same answer for the given rational number as well.
Other Examples: `3/(7) = (21)/(49)`, `3/(13) = 9/(39)`, `2/(3) = (3)/(9)` etc...
3. If the number is not in proper fraction format, convert it into proper fraction so we separate the integer part and the fraction part.
Other Examples: `(99)/(49) = 2(1)/(49)`, `16/(13) = 1(3)/(13) = 1(9)/(39)` etc...
4. For every number that ends in 9, we can associate a new number called Ekadhika for that number. Let's find that ekadhika for b9. The Ekadhika number for denominator `(b9)` is nothing but "anything before the one's place plus 1". In the case of 19, it is 1+1 = 2
Remember the Ekadhikina rule - which is nothing but “By one more than the previous one”
So, In our case, the Ekadhika for 19 is 1+1 = 2
Other Example:
Ekadhika for 7 in `3/(7) = (21)/(49)` is 4+1 = 5
Ekadhika for 3 in `3/(13) = 9/(39)` is 3+1 = 4 etc...
5. These are proper fractions. So the answers will be starting with zero as the integer portion and what we are going to find will be all numbers after decimal. So lets start with `0.` marked.
Note: If we had a improper fraction, we would have put that Integer value instead of zero before decimal.
Perform Step 6 or Step 7 as your choice of operation
Division Method with Ekadhika Number
6. Once we get the Ekadhika, then it is divison time. We start doing a recursive division starting with ` ( "numerator" )/(ekadhika) `. Append the values recursively.
**Pay special attention to how we write the quotient and reminder for these divisions**
| Step | Step Answer | Overall Answer |
| ` ( "numerator" )/(ekadhika) = 1/2` | Quotient (Q) = 0 Reminder (R) = 1 |
`1/(19) = ` `0._1 0` |
| The reminder is always written before the quotient in a subscripted format like above. | ||
| ` ( RQ )/(ekadhika) = (10)/2` | Q = 5, R = 0 | `1/(19) = ` `0._1 0_0 5` |
| The reminder & quotient are read together as a single number that means this in this case, it is 10 (RQ = 10). Now divide this with Ekadhika and find the new Q & R | ||
| ` ( RQ )/(ekadhika) = (05)/2` | Q = 2, R = 1 | `1/(19) = ` `0._1 0_0 5_1 2` |
| ` ( RQ )/(ekadhika) = (12)/2` | Q = 6, R = 0 | `1/(19) = ` `0._1 0_0 5_1 2_0 6` |
| ` ( RQ )/(ekadhika) = (06)/2` | Q = 3, R = 0 | `1/(19) = ` `0._1 0_0 5_1 2_0 6_0 3` |
| ` ( RQ )/(ekadhika) = (03)/2` | Q = 1, R = 1 | `1/(19) = ` `0._1 0_0 5_1 2_0 6_0 3_1 1` |
| ` ( RQ )/(ekadhika) = (11)/2` | Q = 5, R = 1 | `1/(19) = ` `0._1 0_0 5_1 2_0 6_0 3_1 1_1 5` |
| ` ( RQ )/(ekadhika) = (15)/2` | Q = 7, R = 1 | `1/(19) = ` `0._1 0_0 5_1 2_0 6_0 3_1 1_1 5_1 7` |
| ` ( RQ )/(ekadhika) = (17)/2` | Q = 8, R = 1 | `1/(19) = ` `0._1 0_0 5_1 2_0 6_0 3_1 1_1 5_1 7_1 8` |
| ` ( RQ )/(ekadhika) = (18)/2` | Q = 9, R = 0 | `1/(19) = ` `0._1 0_0 5_1 2_0 6_0 3_1 1_1 5_1 7_1 8_0 9` |
| ` ( RQ )/(ekadhika) = (09)/2` | Q = 4, R = 1 | `1/(19) = ` `0._1 0_0 5_1 2_0 6_0 3_1 1_1 5_1 7_1 8_0 9_1 4` |
| ` ( RQ )/(ekadhika) = (14)/2` | Q = 7, R = 0 | `1/(19) = ` `0._1 0_0 5_1 2_0 6_0 3_1 1_1 5_1 7_1 8_0 9_1 4_0 7` |
| ` ( RQ )/(ekadhika) = (07)/2` | Q = 3, R = 1 | `1/(19) = ` `0._1 0_0 5_1 2_0 6_0 3_1 1_1 5_1 7_1 8_0 9_1 4_0 7_1 3` |
| ` ( RQ )/(ekadhika) = (13)/2` | Q = 6, R = 1 | `1/(19) = ` `0._1 0_0 5_1 2_0 6_0 3_1 1_1 5_1 7_1 8_0 9_1 4_0 7_1 3_1 6` |
| ` ( RQ )/(ekadhika) = (16)/2` | Q = 8, R = 0 | `1/(19) = ` `0._1 0_0 5_1 2_0 6_0 3_1 1_1 5_1 7_1 8_0 9_1 4_0 7_1 3_1 6_0 8` |
| ` ( RQ )/(ekadhika) = (08)/2` | Q = 4, R = 0 | `1/(19) = ` `0._1 0_0 5_1 2_0 6_0 3_1 1_1 5_1 7_1 8_0 9_1 4_0 7_1 3_1 6_0 8_0 4` |
| ` ( RQ )/(ekadhika) = (04)/2` | Q = 2, R = 0 | `1/(19) = ` `0._1 0_0 5_1 2_0 6_0 3_1 1_1 5_1 7_1 8_0 9_1 4_0 7_1 3_1 6_0 8_0 4_0 2` |
| ` ( RQ )/(ekadhika) = (02)/2` | Q = 1, R = 0 | `1/(19) = ` `0._1 0_0 5_1 2_0 6_0 3_1 1_1 5_1 7_1 8_0 9_1 4_0 7_1 3_1 6_0 8_0 4_0 2_0 1` |
| After this, the decimals start recurring. We find that by looking that RQ value which is 01 same as the starting value of the numberator. So we stop | ||
So answer is `1/(19) = 0.052631578947368421`
If you chose not to perform step 6, then proceed to perform step 7, to apply this principle.
Multiplication Method with Ekadhika Number
7. Once we get the Ekadhika, then it is multiplication time. We start by writing the numerator as the last digit in the output in the recurring decimal. Then we perform recursive multiplication starting with multiply "latest digit in output" with "ekadhika". Prepend the values recursively.
**Pay special attention to how we write the product and its carryover value for these multiplications**
| Step | Step Answer | Overall Answer |
| "latest digit" = "numerator" = 1 | If numerator had more digits, excess digits will be written as carryover (C). Here C=0 | `1/(19) = ` `?_0 1` |
| "latest digit" (L) x "ekadhika" (E) = 1 x 2 | Product (P) = 2 Carryover (C) = 0 |
`1/(19) = ` `?_0 2_0 1` |
| The carryover is always written before the product in a subscripted format like above. Keep recursively performing ( P x E )+ C | ||
| (L x E) + C ` = (2 " x " 2) + 0` | P = 4, C = 0 | `1/(19) = ` `?_0 4_0 2_0 1` |
| ` = (4 " x " 2) + 0` | P = 8, C = 0 | `1/(19) = ` `?_0 8_0 4_0 2_0 1` |
| ` = (8 " x " 2) + 0` | P = 6, C = 1 | `1/(19) = ` `?_1 6_0 8_0 4_0 2_0 1` |
| ` = (6 " x " 2) + 1` | P = 3, C = 1 | `1/(19) = ` `?_1 3_1 6_0 8_0 4_0 2_0 1` |
| ` = (3 " x " 2) + 1` | P = 7, C = 0 | `1/(19) = ` `?_0 7_1 3_1 6_0 8_0 4_0 2_0 1` |
| ` = (7 " x " 2) + 0` | P = 4, C = 1 | `1/(19) = ` `?_1 4_0 7_1 3_1 6_0 8_0 4_0 2_0 1` |
| ` = (4 " x " 2) + 1` | P = 9, C = 0 | `1/(19) = ` `?_0 9_1 4_0 7_1 3_1 6_0 8_0 4_0 2_0 1` |
| ` = (9 " x " 2) + 0` | P = 8, C = 1 | `1/(19) = ` `?_1 8_0 9_1 4_0 7_1 3_1 6_0 8_0 4_0 2_0 1` |
| ` = (8 " x " 2) + 1` | P = 7, C = 1 | `1/(19) = ` `?_1 7_1 8_0 9_1 4_0 7_1 3_1 6_0 8_0 4_0 2_0 1` |
| ` = (7 " x " 2) + 1` | P = 5, C = 1 | `1/(19) = ` `?_1 5_1 7_1 8_0 9_1 4_0 7_1 3_1 6_0 8_0 4_0 2_0 1` |
| ` = (5 " x " 2) + 1` | P = 1, C = 1 | `1/(19) = ` `?_1 1_1 5_1 7_1 8_0 9_1 4_0 7_1 3_1 6_0 8_0 4_0 2_0 1` |
| ` = (1 " x " 2) + 1` | P = 3, C = 0 | `1/(19) = ` `?_0 3_1 1_1 5_1 7_1 8_0 9_1 4_0 7_1 3_1 6_0 8_0 4_0 2_0 1` |
| ` = (3 " x " 2) + 0` | P = 6, C = 0 | `1/(19) = ` `?_0 6_0 3_1 1_1 5_1 7_1 8_0 9_1 4_0 7_1 3_1 6_0 8_0 4_0 2_0 1` |
| ` = (6 " x " 2) + 0` | P = 2, C = 1 | `1/(19) = ` `?_1 2_0 6_0 3_1 1_1 5_1 7_1 8_0 9_1 4_0 7_1 3_1 6_0 8_0 4_0 2_0 1` |
| ` = (2 " x " 2) + 1` | P = 5, C = 0 | `1/(19) = ` `?_0 5_1 2_0 6_0 3_1 1_1 5_1 7_1 8_0 9_1 4_0 7_1 3_1 6_0 8_0 4_0 2_0 1` |
| ` = (5 " x " 2) + 0` | P = 0, C = 1 | `1/(19) = ` `0._1 0_0 5_1 2_0 6_0 3_1 1_1 5_1 7_1 8_0 9_1 4_0 7_1 3_1 6_0 8_0 4_0 2_0 1` |
| After this, the decimals start recurring. We find that by looking that (L x E) + C ` = (0 " x " 2) + 1 = 1` value which is same as the starting value of the numerator. So we stop | ||
So answer is `1/(19) = 0.052631578947368421`
Amazing isn’t it? Who would have thought of doing multiplication for finding an output for division! Even if you choose division method, we are not dividing with the complex number 19 but with 2 and yet we get the answer we were looking for!
Algebric Proof for Ekadhika Method
Are we sure that this method will work correctly? Or is it Vedic Math steps a mere coincidence?
Though the steps might seem so absurdly simple, internally Vedic Math follows every single mathematical principle and there is absolutely no deviation in that.
Like previous post, lets see the Algebric Proof for this as well.
Let the rational number A = `a/(b9)` and x = 10
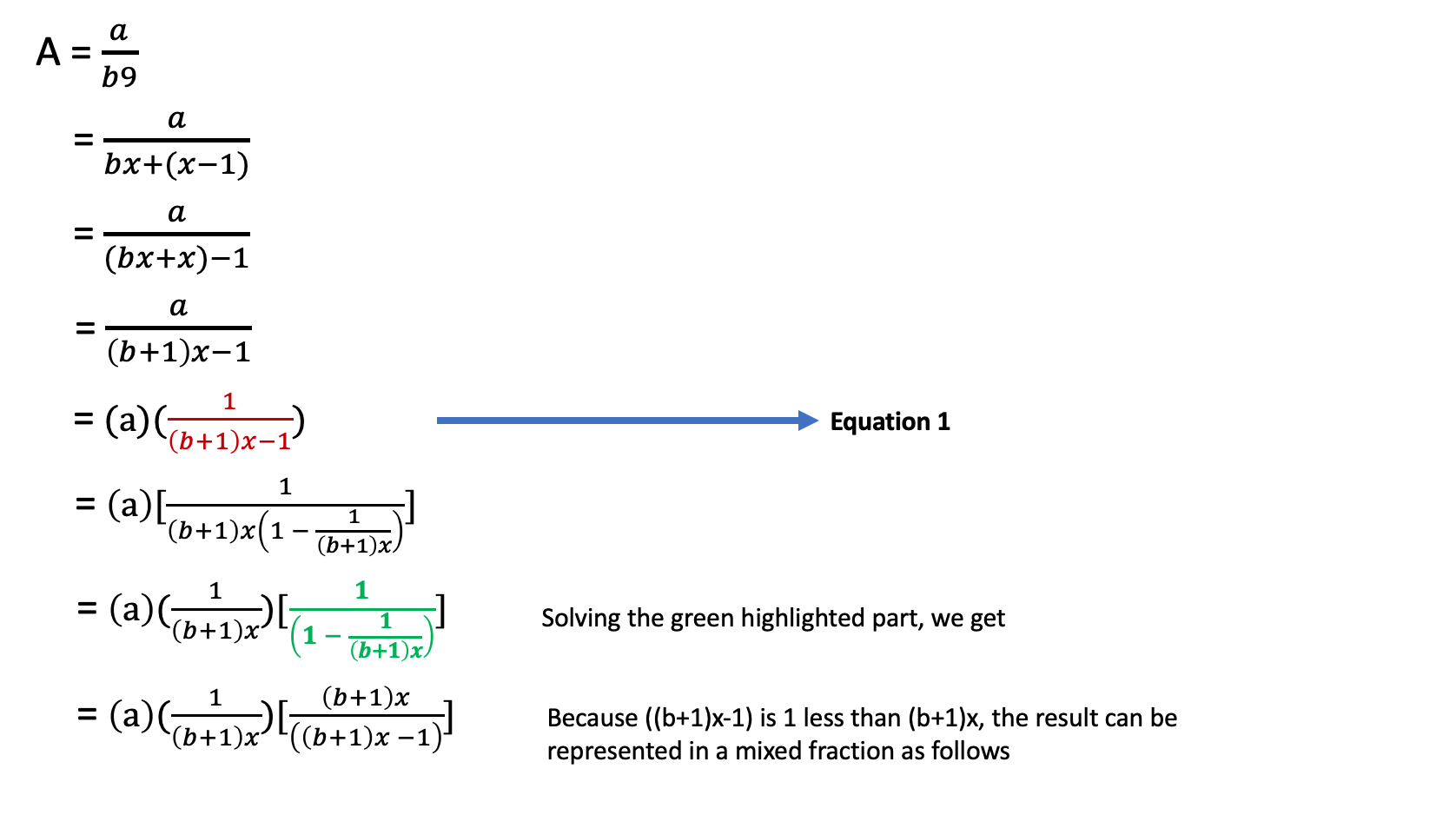


Conclusion
So lets conclude the post by finding the answer for the question.
Find the value of `3/13`?
`3/(13) = 9/(39)` in equivalent rational number.
Ekadhika is 4 for 13.
`3/(13) = 9/(39) = ` `0._1 2_0 3_3 0_2 7_3 6_0 9`
That concludes this week’s post on Ekadhika. See you next week with yet another interesting Vedic method for problem solving.
Until then, Happy Math!

 Never miss a story from us, subscribe to our newsletter
Never miss a story from us, subscribe to our newsletter