Square a given number using Vedic Math

Use Indian Vedic Techniques to excel in Math

Introduction

Hello everyone!, Let’s jump right away into understanding how Vedic Principle makes it very easy and intuitive to understand and perform squaring of a given number.

The Vedic principle that we will use to solve this is called “Urdhva Tiryagbyham” which simply means “Vertically and crosswise”

Can you square this number mentally in few seconds?

2243565² = ?

Try it the conventional way and you will find how time consuming it is!

How to apply Urdhva Tiryagbyham principle?

Let us take an examples and see what kind of operations we are performing for squaring in regular method. Also let’s then understand, how “Vertically & Crosswise” method identifies the patterns and extracts them into easy to perform simple operations.

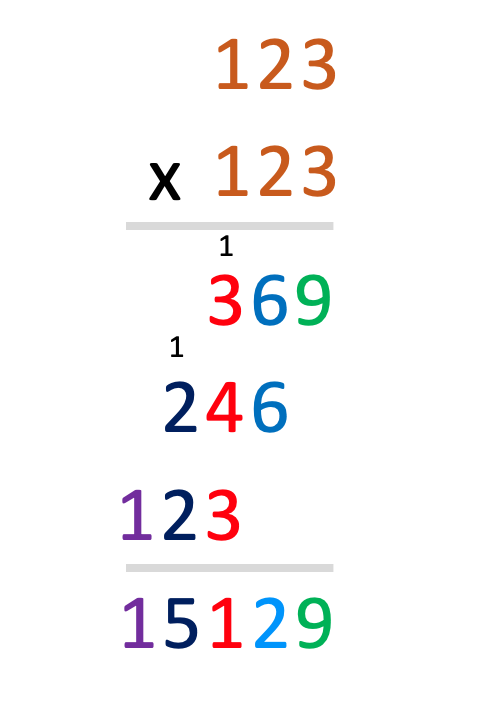
Example: Square of 123? After some calculations, we say it is 15,129.

Now look at the steps that we perform in a regular method as below.

Observations:

1. We see the total digits for the result is 5 (Squared answer will have total digits as >= twice the length of digits in the squaring number - 1)
2. Since we had 3 digits in the input number, we have three rows of individual digits multiplications and carryovers (Regular Method Steps)

Let’s look at how each of the 5 digits in the output is formed. What are the various multiplications that we performed betweent the digits of the two numbers inorder to arrive at the final answer. Lets go from Left to Right. Refer the picture below.

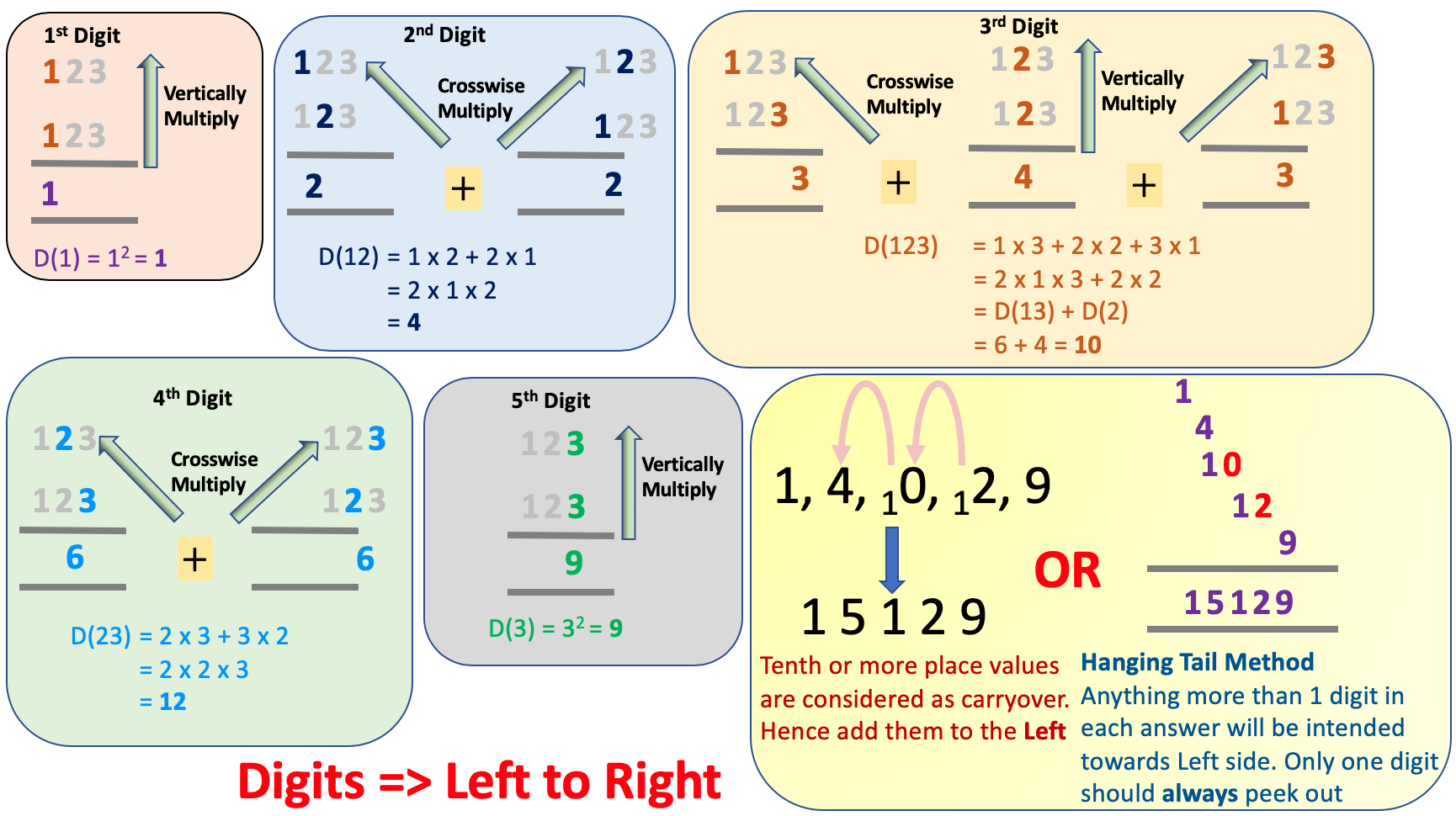
Looking at the picture it is evident that there is a pattern that is hidden in these multiplications.

1st Digit - It is a mere vertical multiplication of the 100th place value digits.

2nd Digit - It is a sum of crosswise multiplication of 100th & 10th place value digits both ways.

3rd Digit - It is a sum of crosswise multiplication of 100th & Units place value digits both ways along with addition to the square of the 10th place.

4th Digit - It is a sum of crosswise multiplication of 10th & Units place value digits both ways.

5th Digit - It is a mere vertical multiplication of the Units place value digits.

We call the process of finding output individual for each output digit as Duplex process.

We write that as D(). The vedic principle understands this inherent pattern and exploits it to full use. Infact helps to extend it to as many digits as you want.

See the picture again for the square of 123. How Vertically and Crosswise helps get individual digit place answer. Once you have them, then it is mere carryover addition.

I personally like to use the hanging tail method (That’s what I am calling it!). We know that every place value should have only one digit. Anything more than that will be carryover to the left. Thats exactly what we are doing here by arranging such that always only one number is peeking out in every row. Everything else is indented inside.

How do we extend this Principle

Its a very simple process. I call it has “Append & First in first out”.

What I mean is, first start writing the number from Left onwards to find Duplex individually. Refer the generalization picture given below while following the steps.

1. Suppose you want to find abcdefgh² ?
2. First write the left most digit alone. D(a) = ?
3. Next add the immediate right digit to it and create a new Duplex row. D(ab) = ?
4. Keep on adding one number from Right until you complete the entire series of digits given to you.
5. Then start deleting the numbers from the Left one at a time and rewrite the entire remaining digits as new duplex row.
6. Do this until you are left with only the One’s place digit
7. Find the Duplex values for all these rows individually.
8. While finding it, use this simple rule of thumb (Inherent relationship extracted by Vedic Principle. Refer the example for 123² if need to understand these relationships again)
   1. If the row contains 1 digit, then Duplex is the square of the number. D(a) = a²
   2. If the row contains 2 digit, then Duplex is twice the product of the digits. D(ab) = 2ab
   3. If the row contains 3 digits, then Duplex is the twice the product of the first and last digits plus square of the middle number. D(abc) = 2ac + b²
   4. If it contains more digits, you just need to create matching pairs working your way through from the extreme ends pairing left and right digits. All these pairs will be multiplied and doubled while any middle number leftover will be squared. Add all of these outputs to get the final Duplex value for that row.

Even for a seemingly complex number with n digits, this process will help you break the number into small pieces that you can do all these calculations in mind. Infact, once you start using this method, you can compute the square in one single line.

Conclusion

So lets conclude the post by finding the answer for the question. See below the calculation and the detailed steps to arrive at the answer.

224356² = 50335614736

That concludes this week’s post on Vedic Math. See you next week with yet another interesting Vedic method for problem solving.

Until then, Happy Math!