Speed Multiplication using Vedic Math

Use Indian Vedic Techniques to excel in Math

Introduction

Hello everyone!, Now that we have completed the “All from 9 and Last from 10” and “Proportionality” principles, let’s dive into the next principle in Vedic Math - “Ekadhikina Purvena” which means “By one more than the previous one”.

It has multiple applications. In this post, we will see how it can help quickly

1. Calculate square of a given number ending in 5
2. Product of two numbers who’s unit digits add to ten and have the same place value for the other digits.

Also in the subsequent posts, we will apply it to other areas such as finding recurring decimals.

So let’s continue our vedic math journey.

Can you solve these problems mentally in few seconds?

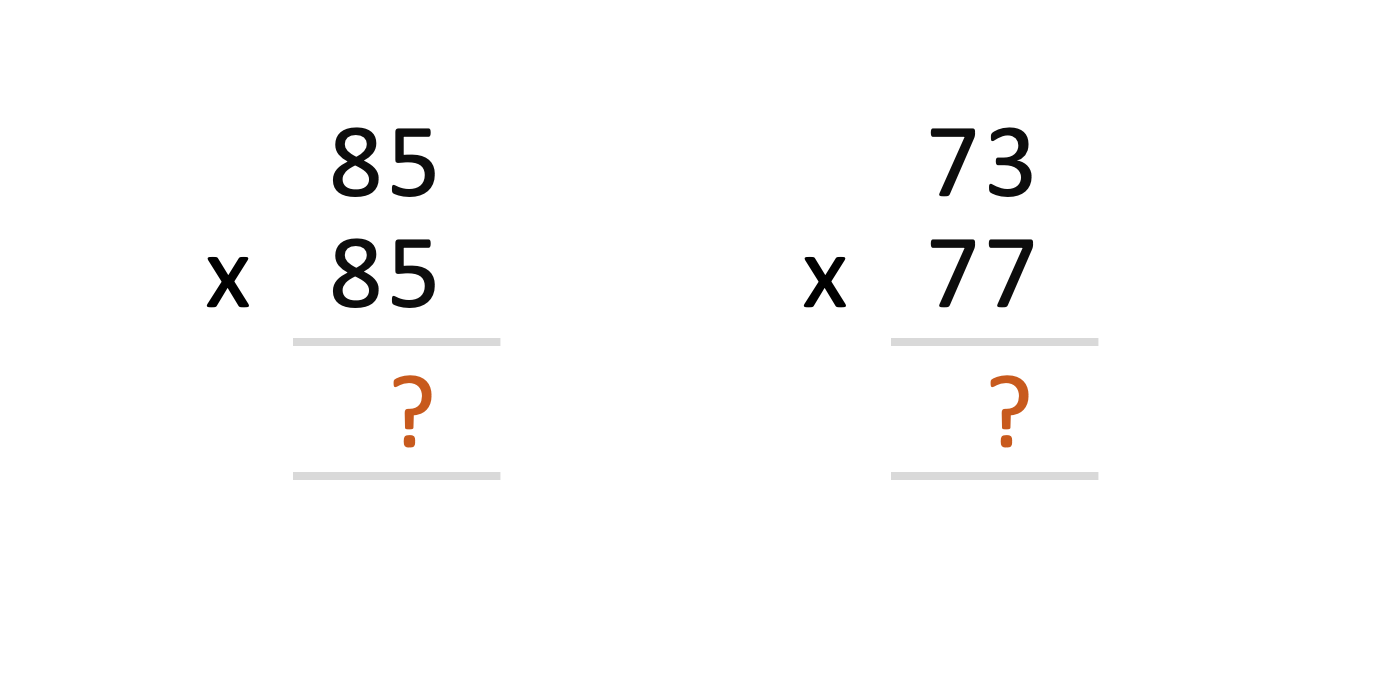
If you are interested in finding this out, pls read on.

What is Ekadhikina Sutra ?

“Ekadhikina Purvena” which means “By one more than the previous one”. So all it says is add one more to the number than it was before.

For example, per Ekadhikina rule, for a given number say 35, the Ekadhikina value for 3 is 4 (3 + 1).

Let’s see how this principle is used to solve the two problem statements that we took upon

1. Calculate square of a given number ending in 5
2. Product of two numbers who’s unit digits add to ten and have the same place value for the other digits.

How the Method Works?

For both the problems, the method is exactly the same.

Let’s take the below two examples.

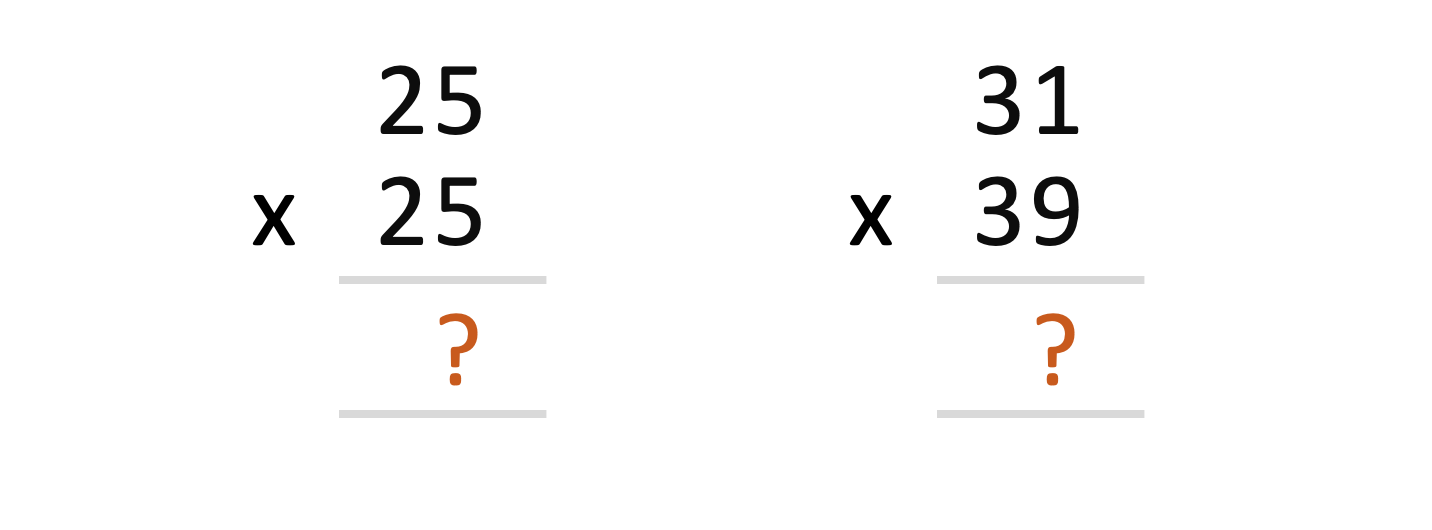
Steps to solve:

1. Your answer is divided into two parts. Left side portion and Right side portion.
2. Take the unit digits. Multiply them and write them as your answer’s right side portion.
   1. If you consider for squaring the number ending in 5, this multiplication is always 25.
   2. The right side answer should be represented as a two digit number.
   3. If you dont have two digit, a leading zero should be added.
3. Your all other digits on the left side are same for both the numbers.
4. Take that number and multiply it with one more than itself. This is the Ekadhikina rule.
5. Write the outcome as your left side portion of your answer.
6. There you go, you got the answer!

Let’s apply these steps for the examples that we took.

Squaring 25

See how we have split the right and left side to arrive at the answer so quickly.

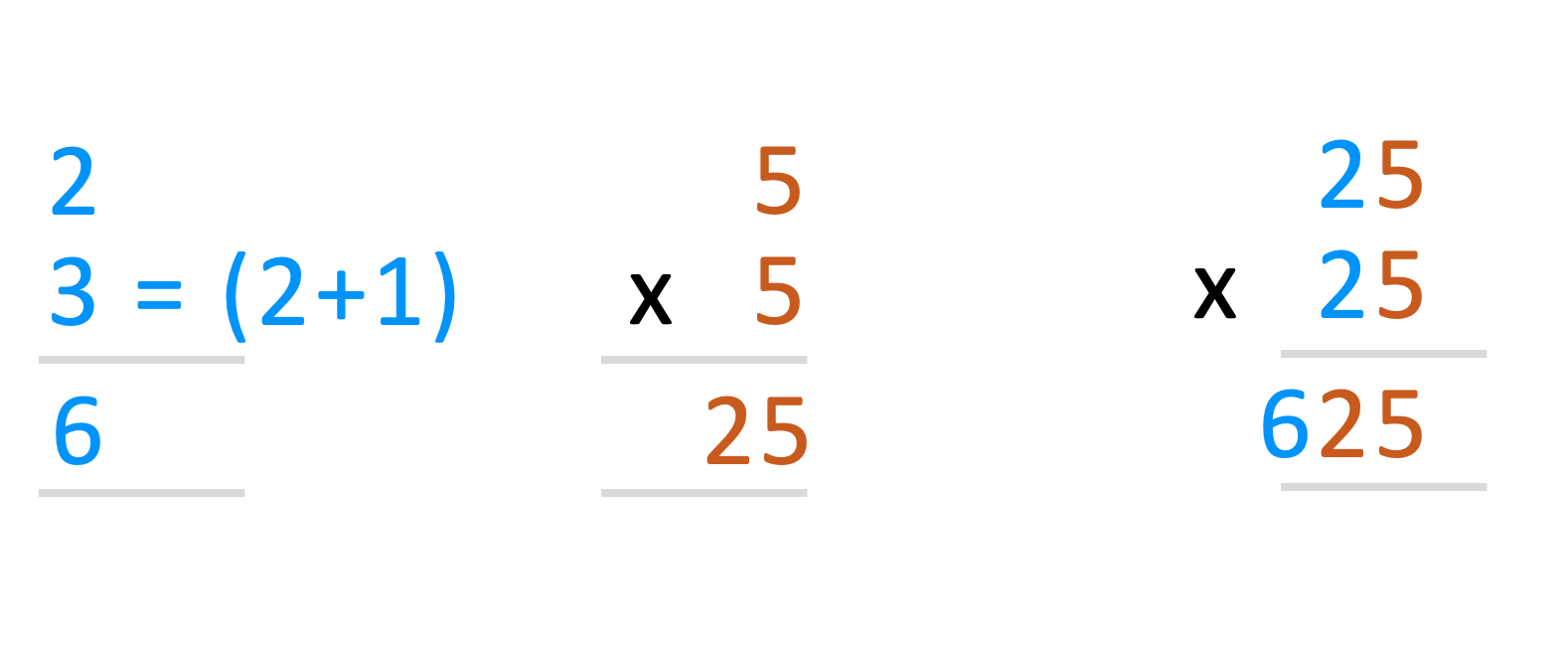
Multiply 31 x 39

The same method is applied here as well to achieve the desired result.

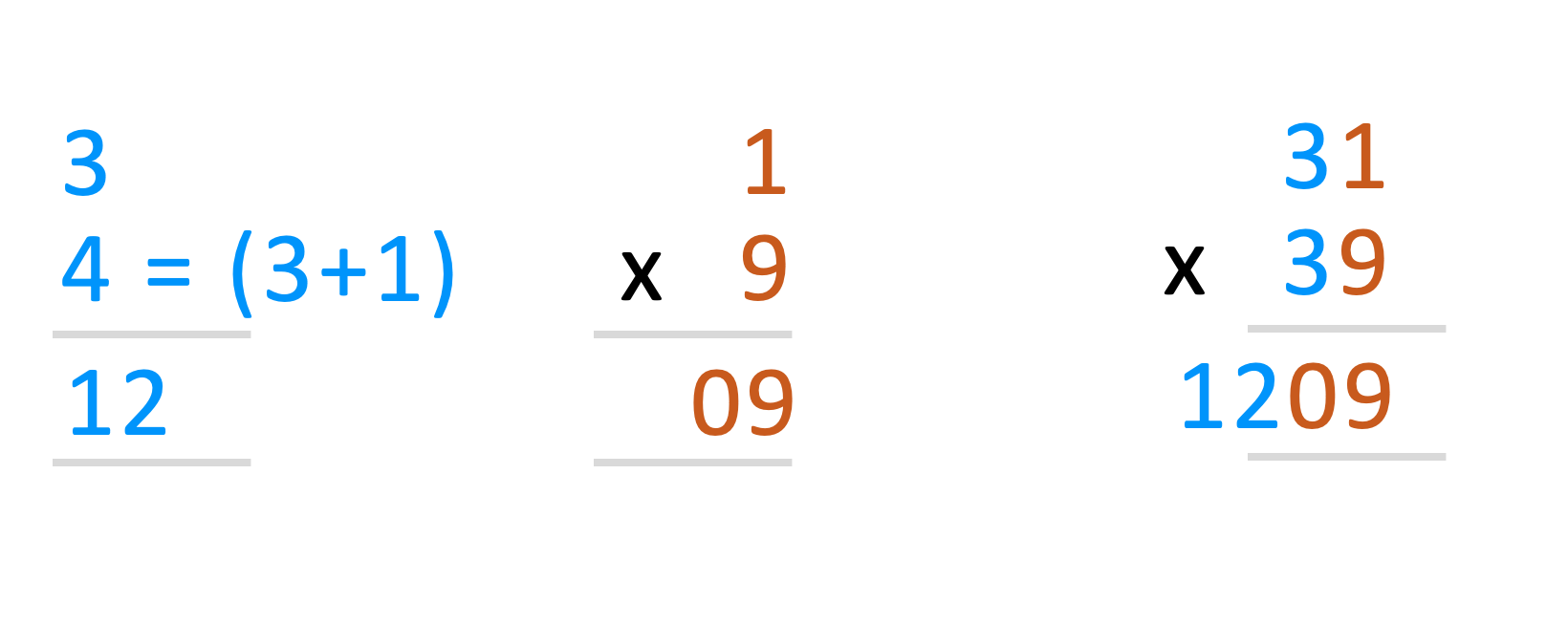
Algebric Proof for Ekadhikina Application

We will see both the variations of the proof. Although the first one is a special case of the second scenario that we discussed.

For Squares ending in 5

Let the number to be squared be
A = (ax + 5)
Where x = 10 and ax represents the value A-5  

So A2 = (ax + 5)2
                 = (ax)2 + 2(ax)(5) + 52
                 = a2x2 + 10(ax) + 25
                 = a2102 + 10(a10) + 25
                 = 102(a2 + a) + 25
                 = 102a(a + 1) + 25

Isn’t it what we are also doing - (a)(a+1) as left side and 25 as right side of the answer. The left side value is multiplied by 100 which is why, we conveniently just merge right and left side.

For numbers with unit digits adding to 10 and other place values being same

Let the numbers to be muliplied be
A = (cx + a)
B = (cx + b)
Where
x = 10
cx represents the value A-a  
cx represents the value B-b  
a + b = 10

So A.B           = (cx + a)(cx + b)
                 = (cx)2 + cxb + cxa + ab
                 = (cx)((cx) + b+a) + ab
                 = (cx)((cx) + 10) + ab
                 = (cx)((cx) + x) + ab
                 = x2c(c+1) + ab
                 = 102c(c+1) + ab                 

And that is why we simply add one to the previous one in Ekadhikina rule.

Conclusion

So lets conclude the post by finding the answer for the initial questions posted.

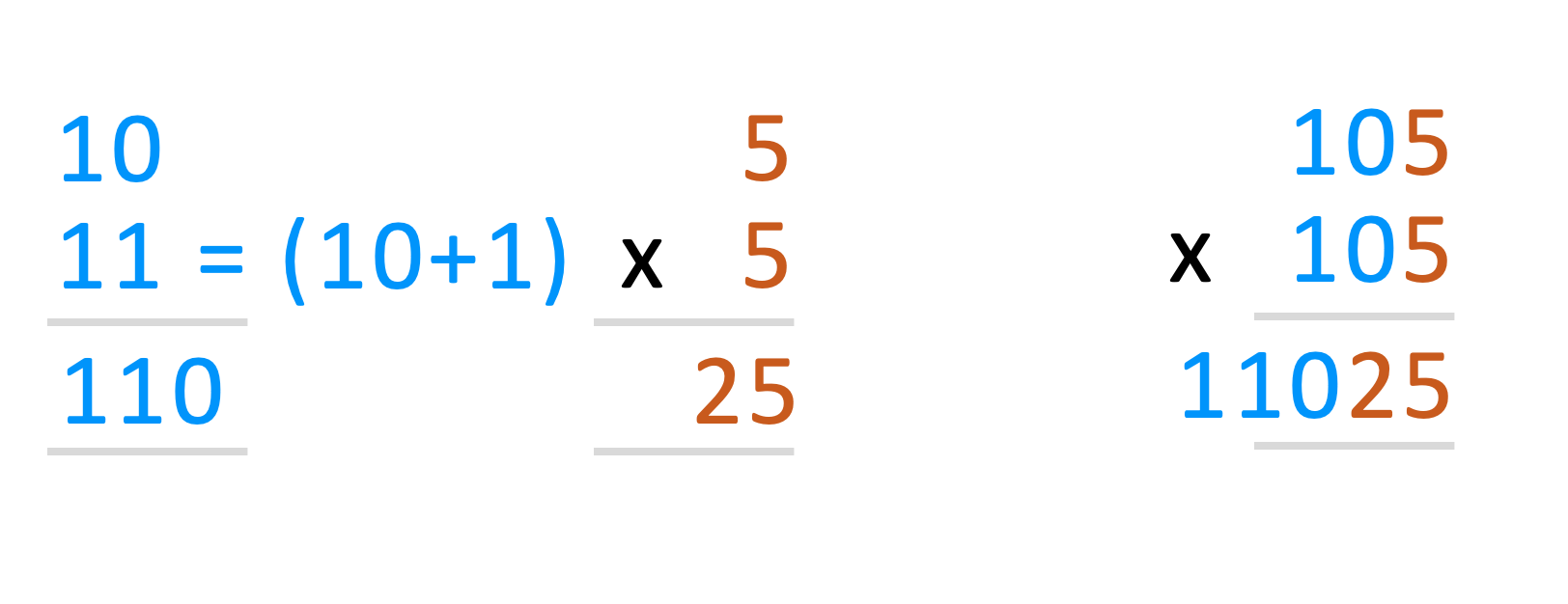
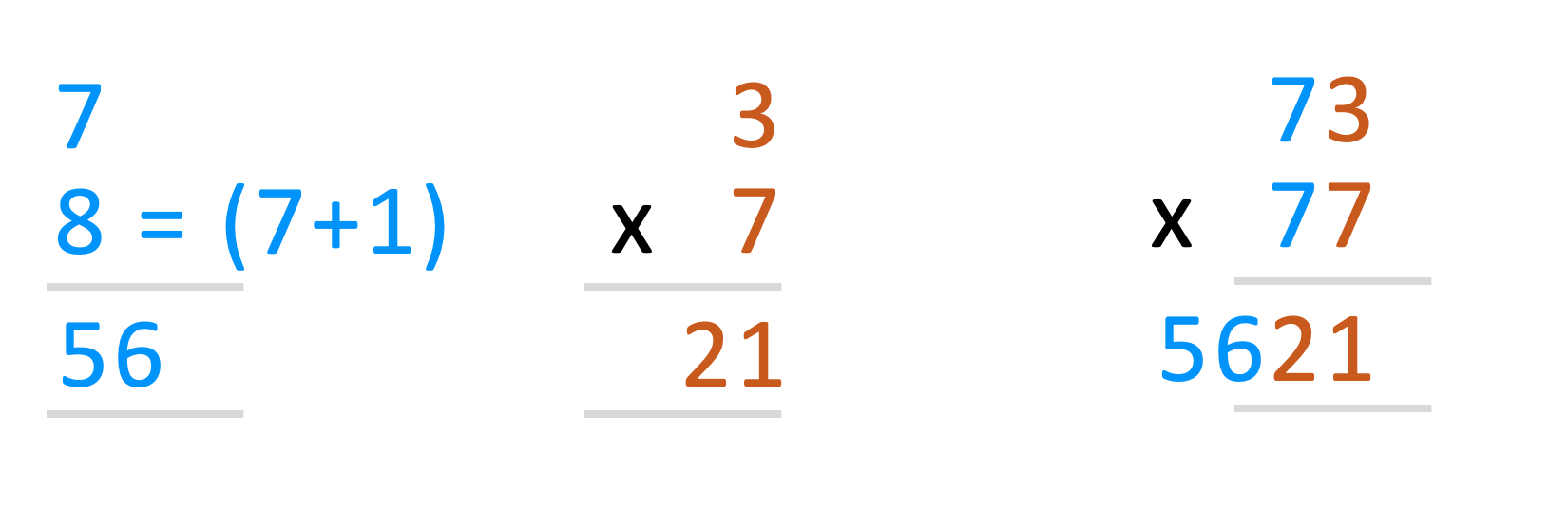
That concludes this week’s post. See you next week with one another interesting application of Ekadhikina rule.

Until then, Happy Math!