Mental Multiplication using Vedic Math - Part 1

Use Indian Vedic Techniques to excel in Math
Introduction
This series of post are to educate on how to utilize the powerful and simple Sutras (Rules) of Ancient Indian Math called “Vedic Math” for our day to day Mathematical needs.
Only about 16 Sutras (Rules) and 13 corollaries were able to be saved from getting lost.
One of the 16 Sutras (Rules) is called “Nikhilam Navatashcaramam Dashatah”. It simply means - “All from 9 and the last from 10”.
In this series of posts titled - “Mental Multiplication”, we will look at how this simple principle can be used to quickly do multiplication of two numbers.
Can you do this below multiplication mentally in few seconds ?
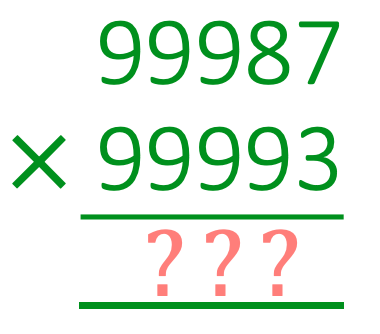
If this interests you, then this series of post is for you. Read on to find out how we can do this in few seconds.
Power of 10 Base
For Nikhilam multiplication, we need to associate numbers close to their corresponding 10x base.
So let’s first understand what these bases mean and how you would represent a given number to its corresponding 10x.
| Number (N) | Nearest 10x | Value of 10x | Difference (N - 10x) |
|---|---|---|---|
| 8 | 101 | 10 | -2 (= 8-10) |
| 13 | 101 | 10 | +3 (= 13-10) |
| 89 | 102 | 100 | -11 (= 89-100) |
| 105 | 102 | 100 | +5 (= 105-100) |
| 225 | 102 | 100 | +125 (= 225-100) |
| 775 | 103 | 1000 | -225 (= 775-1000) |
| 1200 | 103 | 1000 | +200 (= 1200-1000) |
and so on…
So in the Nikhilam Multiplication that we will see soon, we would be referring to these actual numbers and as well as the difference that we calculated from their correponding bases for calculations. Also note the sign for the differences as that is going to play a very important role in multiplication!
What is Nikhilam Sutra ?
“Nikhilam Navatashcaramam Dashatah” simply means “All from 9 and the last from 10”.
The reason it is called “All from 9 and last from 10” is when you try to find the difference between the number and its corresponding base 10x , the last digit is subtracted from 10 and other digits get subtracted from 9. Lets see an example.
Suppose you want to find difference between say 687 and the nearest 10x which is 1000, then to get the difference we subtract the last digit (7) from 10 and the other digits (6 & 8) from 9 each. This gives us 313 which is the difference.
This simple rule can be applied in various flavors to find the multiplication of two numbers. Below are the different variations in which this rule can be applied.
Multiply 2 numbers that are
- less than a common 10x, eg:
89 * 97 - greater than a common 10x, eg:
104 * 109 - near a common 10x, eg:
98 * 109 - near a common proportional of 10x, eg:
303 * 318 - near 2 different 10x, eg:
89 * 10005 - less than 2 different 10x, eg:
89 * 997 - greater than 2 different 10x, eg:
109 * 1004 - near 2 different proportionals of 10x, eg:
205 * 60005
In this post, we will address the first variation. For the rest, we will go through in subsequent posts.
How Nikhilam Method Works?
Lets see how Nikhilam method can do this quicker for the same example.
Example: Find the value of 89 x 97 ?
Nikhilam Method Working:
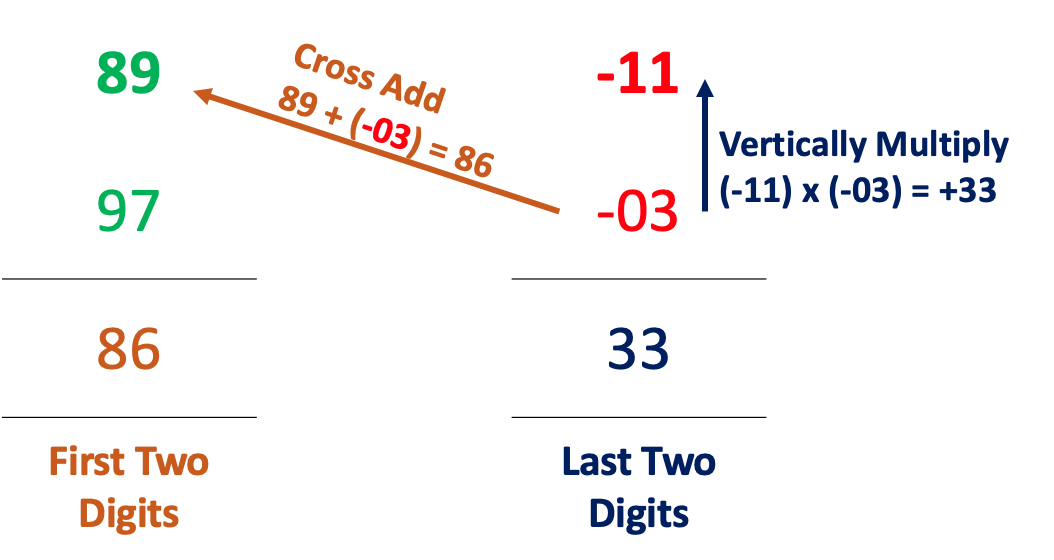
So, 89 x 97 = 8633
Steps to perform the Nikhilam Method:
- Lets first get their corresponding 10x & the difference from 10x.
- Write the numbers that you want to multiply one below the other
- Write the difference between the number and the closest base 10s number on the right side of the number.
- Since the numbers are less than the base, the difference is written as negative numbers
- Now multiply the differences. Both numbers are negative. Hence the multiplication will be a positive number. Based on the base that you have chosen (here we have chosen 100), product of these two differences should be written in as many digits as zeros' in the 10x. Like here product of the difference is 11 * 03 = 33. Since base 100 has 2 zeroes, the answer should be noted in two digits. 33 is a 2 digit number so no issues otherwise we would have to add a leading 0 zeroes to fill that gap. Write the product down.
- Both the numbers on left side are less than the base. Hence you can take any of the difference along with its sign from right side and add it crosswise to the other number on the left. That is either 89 + (-3) or 97 + (-11). Both will yield 86. Write this number down.
- There you go the answer is 8633.
| Actual Numbers to Multiply | Corresponding Difference from 10x |
|---|---|
| 89 | -11 |
| 97 | -03 |
Algebric Proof for Nikhilam Method
Are we sure that this method will work correctly? Or is it just a mere coincidence?
Though the steps might seem so absurdly simple, internally Vedic Math follows every single mathematical principle and there is absolutely no deviation in that.
Lets see that below.
Since the numbers to be multiplied can be represented as (10x - a) lets define the numbers A & B as follows.
Let
A = (10x - a)
B = (10x - b)
So A x B = (10x - a)(10x - b)
= (10x)2 - 10xa -10xb + ab
= (10x)(10x - a) - (10x)b + ab
= (10x)(A) - (10x)b + ab
= (10x)(A - b) + ab
= (10x)(A + (-b)) + ab
This is what we are doing in Nikhilam.
Cross add for first portion of the answer = A + (-b)
Vertically multiply for the last portion of the answer = ab
Isn’t it cool!
Now you will be able to do this math right in your head and you wouldn’t need a calculator or a piece of paper. This can be extended to any higher order base 10s as well. And it will just work very fine.
See below for additional examples:
1
2
3
4
5
498 - 502
x 998 - 002
-----------------
496 1004
------------------
Important: We already said that the right side should have digits equivalent to as many zeros in your base 10x. But here we have 4 digits on the right side whereas the base 10x (1000) has only 3 zeroes. Hence we carry forward the excess digit (1 in this case) to the left side number (496).
So answer is 497004.
1
2
3
4
5
991 - 009
x 998 - 002
-----------------
989 018
------------------
Important: Since 1000 is the (10x) we have chosen, the mulitplication of the differences should be represented in 3 digits (as many zeros in (10x) chosen). Hence leading zero for 18!
So the answer is 989018.
Conclusion
So lets conclude the post by finding the answer for the question.
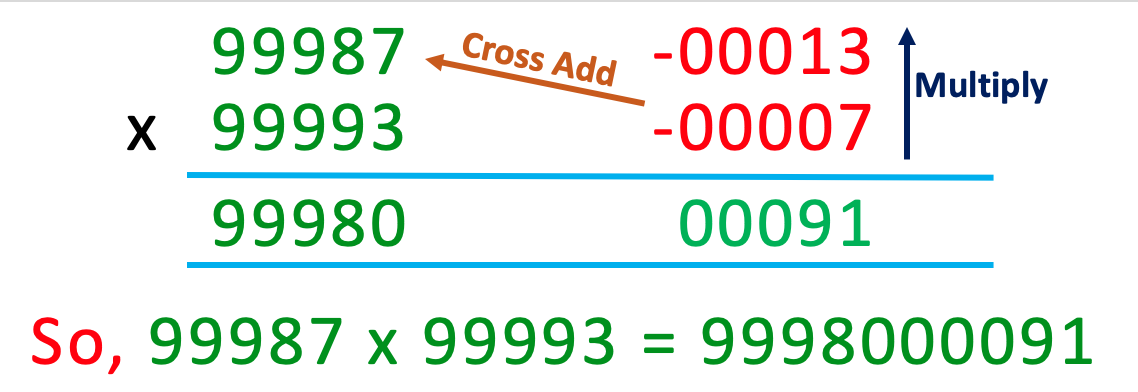
If you were to do this in regular method, it would have been very very laborious. See below.

We will look into the other variations in the subsequent posts. Until then, happy mental math!

 Never miss a story from us, subscribe to our newsletter
Never miss a story from us, subscribe to our newsletter