Mental Multiplication using Vedic Math - Part 4

Use Indian Vedic Techniques to excel in Math
Introduction
This is the part 4 post of the series on “Mental Multiplication using Vedic Math”. Here we will find out on “Multiply 2 numbers that are near a proportional 10x”.
Examples.
- 205 x 209 - The common 10x is 100. But it is 2 times proportional to 100.
- 4982 x 4997 - The common 10x is 1000. But it is 5 times proportional to 1000.
- 69 x 71 - The common 10x is 10. But it is 2 times proportional to 7.
Also note, we are going to do all 3 variations that we so for covered previously in this post for this proportionality variation.
If you need to understand or need a recap of those methods, pls go to the previous posts. You can find all the posts here
We will be using two Vedic Sutras. One we already know - “Nikhilam Navatashcaramam Dashatah” meaning “All from 9 and the last from 10”. The other is the Sub-Sutra (Corollary) called ‘Anurupyena’ means ‘proportionality’. Let us see how we achieve this.
Can you do these below multiplications mentally in few seconds ?
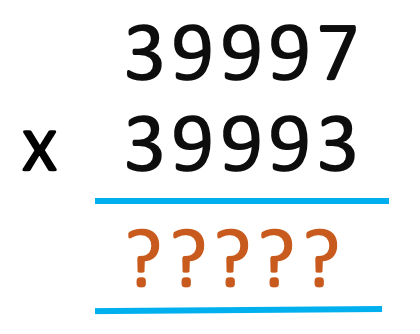

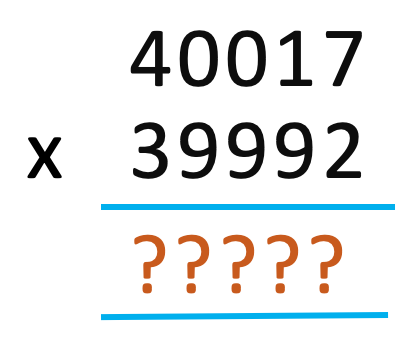
If this interests you, then this series of post is for you. Read on to find out how we can do this in few seconds.
As we already know based on what we learnt from the previous posts that in the Nikhilam Multiplication, the sign for the differences between the number and the base is very critical. It plays important role in when it comes to append the right side value to left side value and well as in the cross add!
Pls refer previous posts, if you need a refresher.
What is Nikhilam Sutra ?
Pls read the previous post here to understand more on this.
What is Anurupyena Sub Sutra ?
We already briefly saw this in the introduction.
To find out the Anurupyena (Proportional Factor or let’s call it as Multiplier), we need to
- Find the 10x that can represent the given number
- Find the multiplier needed to multiply the 10x to bring closer to the given number.
Refer the following table to understand it.
| Number (N) | Representative 10x | Multiplier Needed (m) | Difference (N - m10x) |
|---|---|---|---|
| 86 | 101 | 9 | -4 (= 86-90) |
| 133 | 101 | 13 | +3 (= 133-130) |
| 798 | 102 | 8 | -2 (= 798-800) |
| 50085 | 104 | 4 | +85 (= 50085-50000) |
| 2298 | 102 | 23 | -2 (= 2298-2300) |
Note:
- For 2298, we choose 100 as the value of 10x so we can get the multiplier as 23. If we had chosen 1000 as 10x, then the multiplier is 2.3 which is not what we want.
- Same is the case with 133, we chose 10 instead of 100.
How Nikhilam Method Works?
Let us see, “How to multiply 2 numbers that are near a proportional 10x”.
The same Nikhilam Principles that we studied in the previous posts for
- Both numbers being greater than 10x
- Both numbers being less than 10x
- One number is greater and the other is lesser than 10x can we applied here as well.
The only additional principle that we need to apply is the Multiplier (Proportionality Factor).
Let us see an example.
Example: Find the value of 205 x 209 ?
Nikhilam Method Working:
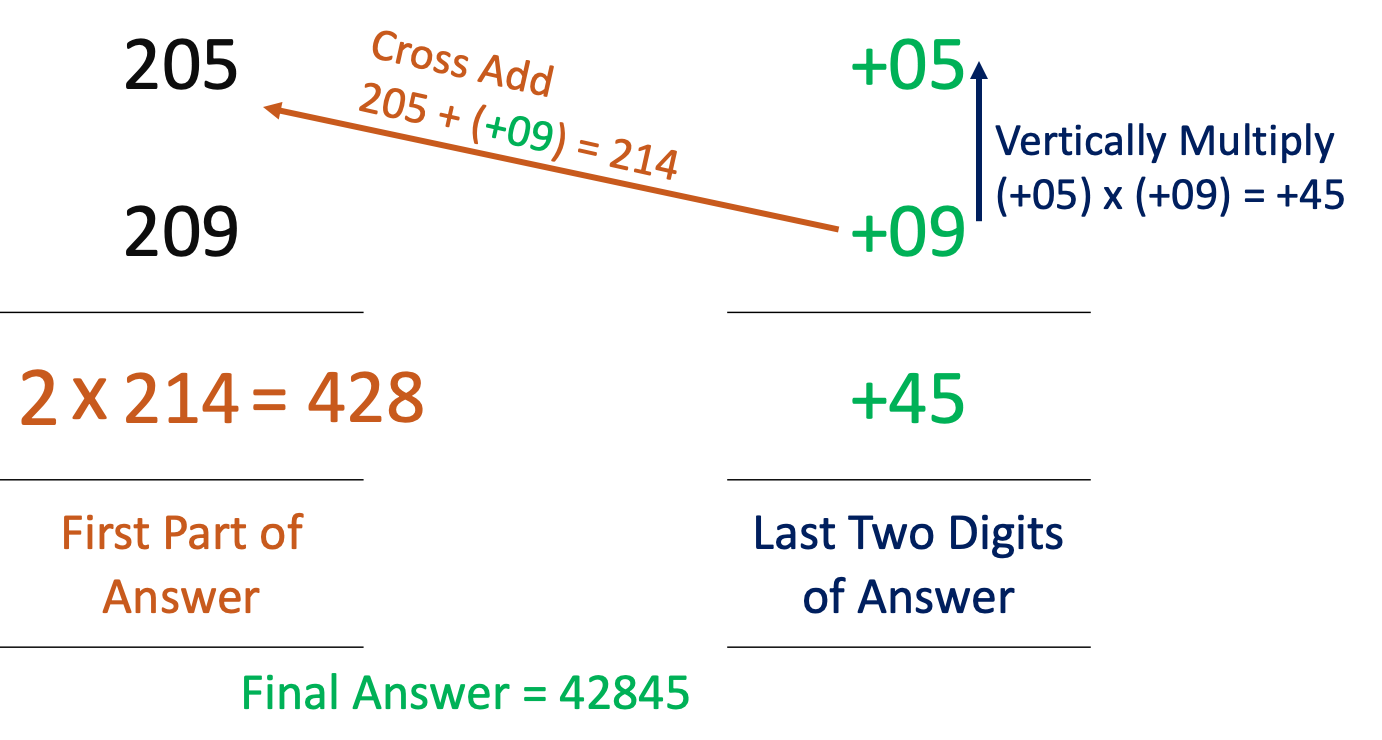
So, 205 x 209 = 42845
Steps to perform the Nikhilam Method:
- Lets first get corresponding 10x, multiplier (m) value & the difference from m10x.
- Write the numbers that you want to multiply one below the other
- Write the difference you just found out on the right side of the number.
- Now multiply the differences. The multiplication will be a positive number. The value is (05 x 09 = 45)
- On the left side, cross add the difference with its sign. Here it is positive so it will be added to the value on the left. Had the difference was negative, then when you add, you will decrease the value from left. Write this number down (+205 + +09 = +214).
- Till this point is the same as Nikhilam
- Mulitply the left side value that you obtained using the Multiplier that you found in the above table. So the value becomes (2 x 214) = 428
- Append the right side value to this new left side value
- There you go, the answer is 42845
| Actual Numbers to Multiply | Multiplier(m)x | Corresponding Difference from 10x |
|---|---|---|
| 205 | 2 | +5 (205 - 2x100) |
| 209 | 2 | +9 (209 - 2x100) |
Algebric Proof for Nikhilam Method
Are we sure that this method will work correctly? Or is it Vedic Math steps a mere coincidence?
Though the steps might seem so absurdly simple, internally Vedic Math follows every single mathematical principle and there is absolutely no deviation in that.
Like previous post, lets see the Algebric Proof for this as well.
Since the numbers to be multiplied can be represented based on (10x) lets define the numbers A & B as follows.
Let
Multiplier = m
A = (m10x + a)
B = (m10x + b)
So A x B = (m10x + a)(m10x + b)
= (m10x)2 + m10xa +m10xb + ab
= m10x(m10x + a) + m10xb + ab
= m10x(A) + m10xb + ab
= m10x(A + b) + ab
This is what we are doing in Nikhilam with Anurupyena.
Cross add for first portion of the answer = (A + b)
Multiplier to multiply the cross addition answer = m(A + b)
Vertically multiply for the last portion of the answer = ab
Isn’t it cool!
The same principle can now be applied to all 3 variations. As long as you take care of the below pointers, the method can be extended to all of the variations.
- The difference with sign
- Identify the correct Multiplier
- Before appending the right side, if it is negative, converting them to positive by performing the borrowing step for BAR Numbers that we saw in post 3
Conclusion
So lets conclude the post by finding the answer for the question.



We will look into the other variations in the subsequent posts. Until then, happy mental math!

 Never miss a story from us, subscribe to our newsletter
Never miss a story from us, subscribe to our newsletter