Mental Multiplication using Vedic Math - Part 5

Mental Multiplication using Vedic Math - Part 5

Use Indian Vedic Techniques to excel in Math

Introduction

This is the part 5 post of the series on “Mental Multiplication using Vedic Math”. Here we will find out on “Multiply 2 numbers that are near 2 different 10x”.

Examples: Variations similar to what we covered in Post 1, 2 & 3 for greater & lesser than 10x.

  1. 105 x 1009 - One number is near 102 and the other is near 103.
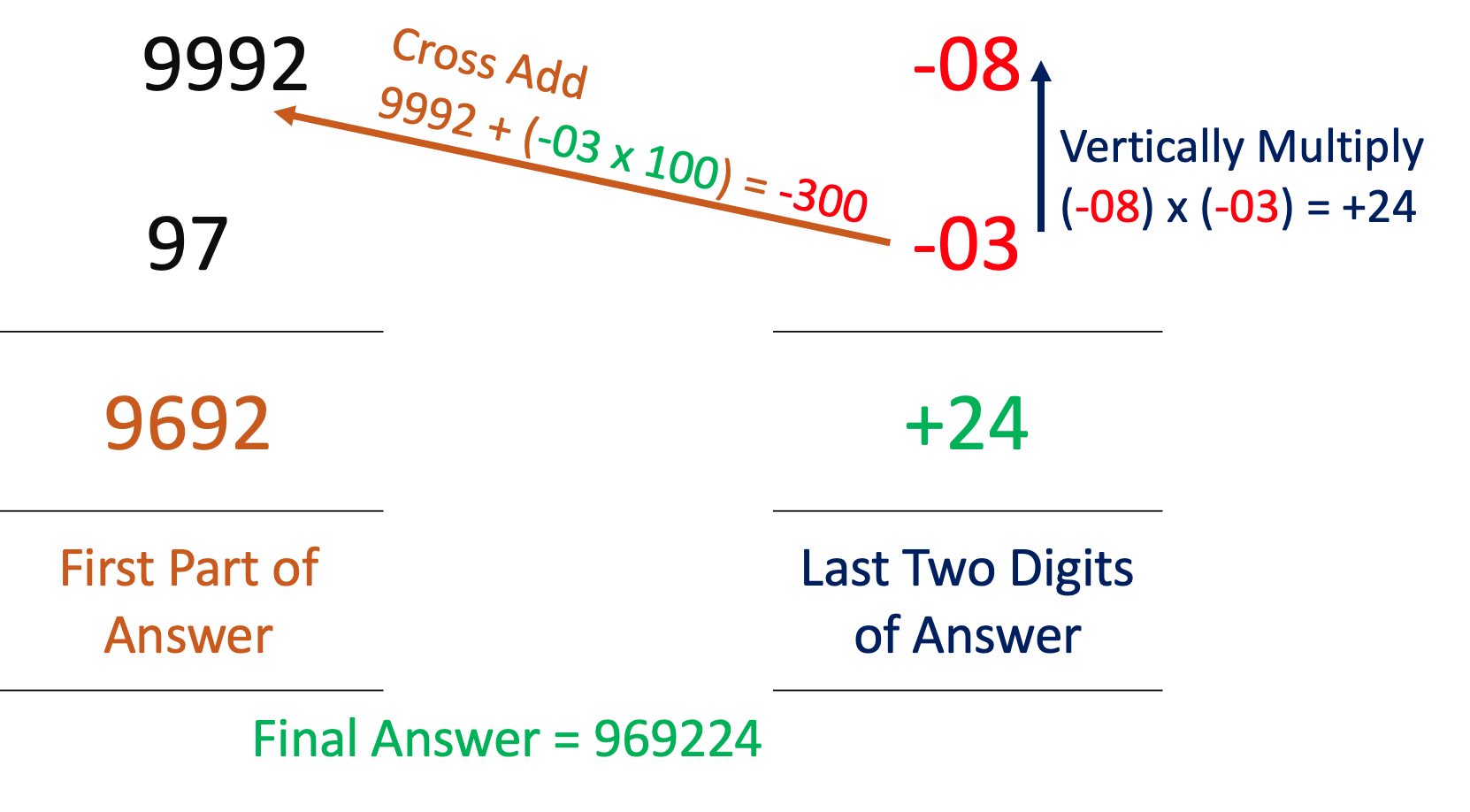
  2. 9992 x 97 - One number is near 104 and the other is near 102.
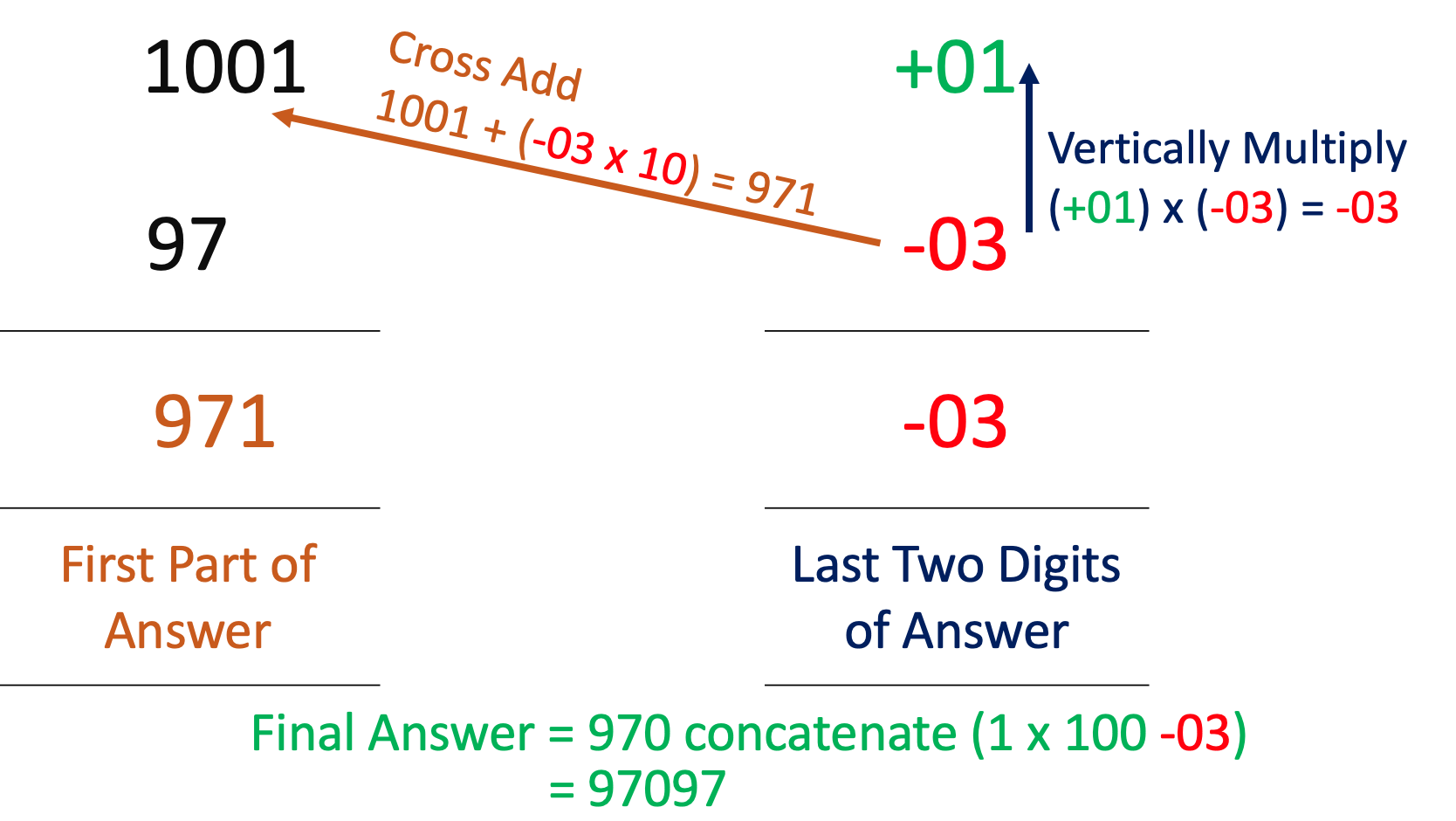
  3. 97 x 1001 - One number is near 102 and the other is near 103

Also note, we are going to do all 3 variations that we so for covered previously in this post for this different base 10x.

If you need to understand or need a recap of those methods, pls go to the previous posts. You can find all the posts here

All the steps you did previously for these 3 variations are same except for one additional step that you need to perform when performing the CROSS ADDITION step.

Can you do these below multiplications mentally in few seconds ?

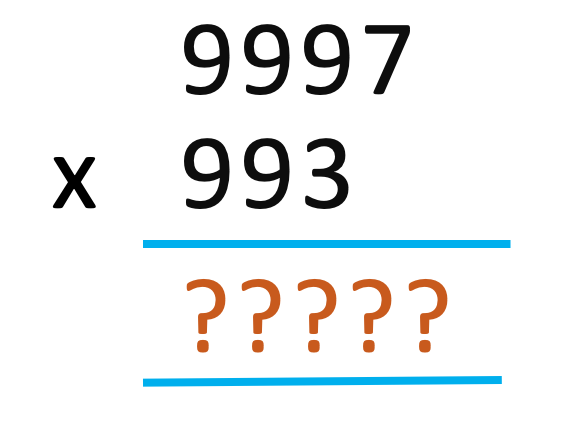
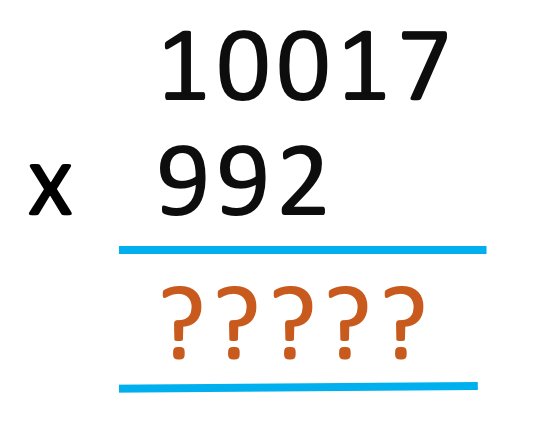
If this interests you, then this series of post is for you. Read on to find out how we can do this in few seconds.

As we already know based on what we learnt from the previous posts that in the Nikhilam Multiplication, the sign for the differences between the number and the base is very critical. It plays important role in when it comes to append the right side value to left side value and well as in the cross add!

Pls refer previous posts, if you need a refresher.

What is Nikhilam Sutra ?

Pls read the previous post here to understand more on this.

How Nikhilam Method Works?

Let us see, “How to multiply 2 numbers that are near 2 different 10x”.

The same Nikhilam Principles that we studied in the previous posts for

  1. Both numbers being greater than 10x
  2. Both numbers being less than 10x
  3. One number is greater and the other is lesser than 10x can we applied here as well.

The only additional principle that we need to apply is we need a 10x-y CrossMultiplier (cm) = (10x-y) (Proportionality Factor) for cross addition.

Let us see an example.

Example: Find the value of 1009 x 105 ?

The first number is 1009. Its base 10x = 103. So we can say x = 3. The second number is 105. Its base 10y = 102. So we can say y = 2. The CossMultiplier that we need to use for the difference getting added to left side number is going to be 10x-y = 103-2 = 101.

Let’s find understand the

Nikhilam Method Working:

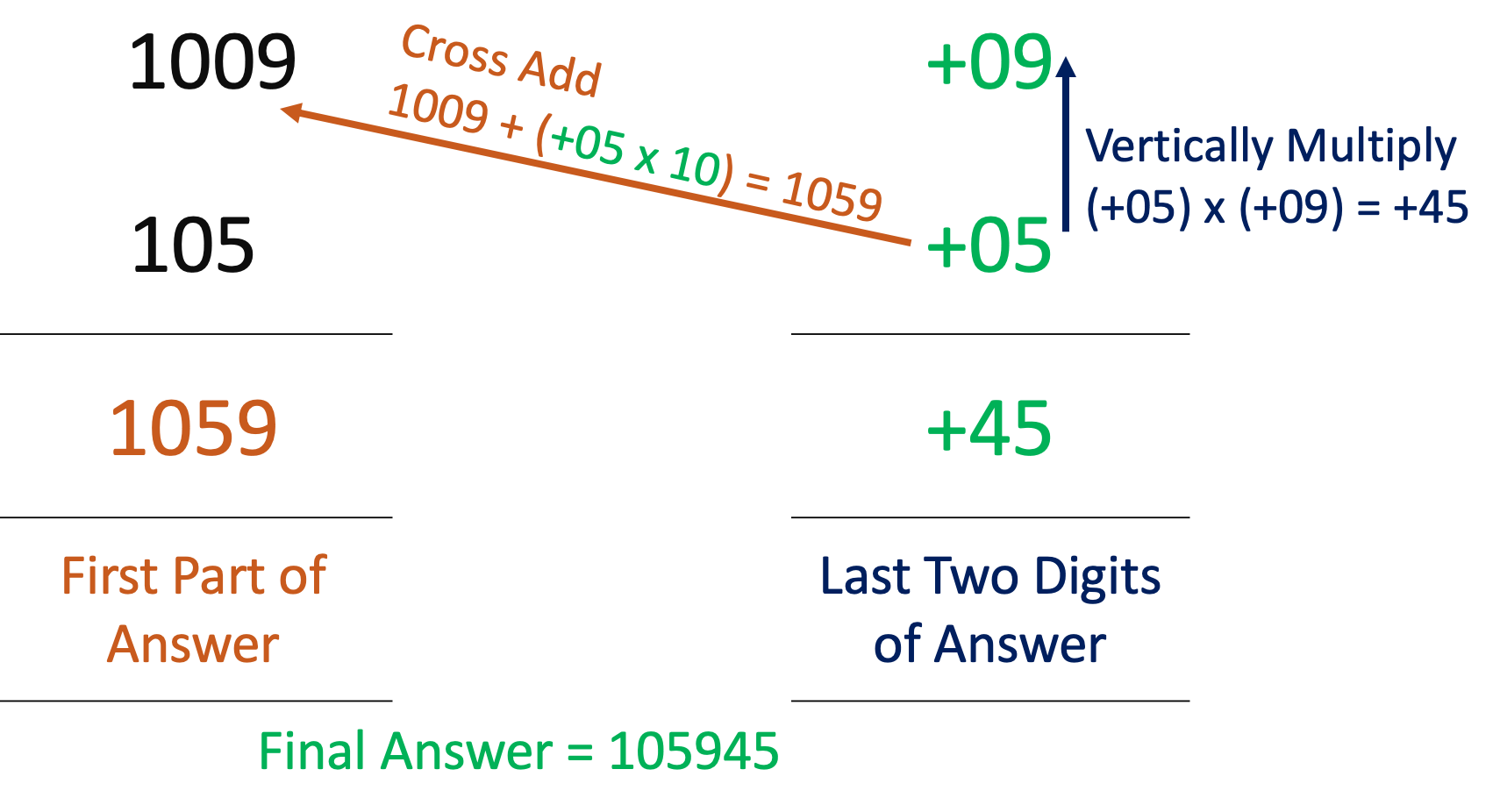
So, 1009 x 105 = 105945

Steps to perform the Nikhilam Method:

  1. Lets first get corresponding 10x, crossmultiplier (cm) value & the difference from 10x respectively
    2. Actual Numbers to Multiply CrossMultiplier(cm)x Corresponding Difference from 10x
    1009 103-2 = 101 +9 (1009 - 1000)
    105 102-3 = 10-1 +5 (105 - 100)
    Note: So far, we were saying CROSS ADD can be done both ways. Its still true. However, it is best to avoid the direction where the CrossMultiplier value is in decimal. Like look at the second row, the CM value = 10-1 = 0.1. Remember our intention is to do all these math mentally and faster, so AVOIDING the decimals for multiplication would be best. But incase you still want to pursue you can go ahead. The answer should still be the same as long as the left and right side are appended correctly.
  2. Write the numbers that you want to multiply one below the other
  3. Write the difference you just found out on the right side of the number.
  4. Now multiply the differences. The multiplication will be a positive number. The value is (09 x 05 = 45)
  5. Also note the important point. The mulitplication answer on the right side should have as many digits equivalent to the number of zeros in the least power between 10x & 10y. In this case it is y = 2 is the least. So the answer should have 2 digits. If not, prefix it with zeros to fill the count
  6. To the left side, cross add the difference with its sign. But before you add it, you need to multiply the difference with Cross Multiplier value you found out. So that would be like this. 1009 + (5 x 101) = 1059. Write this number down.
  7. Append the right side value to this new left side value
  8. There you go, the answer is 105945

Same way is what we are performing the other 2 variations. Sample examples are provided below for better understanding.

Variation 2:

Variation 3:

Algebric Proof for Nikhilam Method

Are we sure that this method will work correctly? Or is it Vedic Math steps a mere coincidence?

Though the steps might seem so absurdly simple, internally Vedic Math follows every single mathematical principle and there is absolutely no deviation in that.

Like previous post, lets see the Algebric Proof for this as well.

Since the numbers to be multiplied can be represented based on (10x) lets define the numbers A & B as follows.

Let the numbers be
A = (10x + a)
B = (10y + b)
Also x > y.

So A x B = (10x + a)(10y + b)
         = (10x+y) + 10ya +10xb + ab
         = 10y(10x + a) + 10xb + ab
         = 10y(A) + 10xb + ab  
         = 10y(A + 10x-yb) + ab

This is what we are doing in Nikhilam with Anurupyena.
Cross add for first portion of the answer = (A + 10x-yb)
Vertically multiply for the last portion of the answer = ab

Isn’t it cool!

Conclusion

So lets conclude the post by finding the answer for the question.




That concludes our series on Mental Math using Nikhilam Method.

The only pending variation is to combine Anurupyena as well on top of this variation that we just saw in this post.

I will leave that to you to deduce on your own. Should you need help, dont forget to comment and we can solve it.

Happy Math! See you soon in the next Sutra of Vedic Math!

Kadiresan Dhanasekaran
Kadiresan Dhanasekaran
An avid learner
comments powered by Disqus